34.1 Cosmology and Particle Physics – College Physics

Look at the sky on some clear night when you are away from city lights. There you will see thousands of individual stars and a faint glowing background of millions more. The Milky Way, as it has been called since ancient times, is an arm of our galaxy of stars—the word galaxy coming from the Greek word galaxias, meaning milky. We know a great deal about our Milky Way galaxy and of the billions of other galaxies beyond its fringes. But they still provoke wonder and awe (see Figure 1). And there are still many questions to be answered. Most remarkable when we view the universe on the large scale is that once again explanations of its character and evolution are tied to the very small scale. Particle physics and the questions being asked about the very small scales may also have their answers in the very large scales.

As has been noted in numerous Things Great and Small vignettes, this is not the first time the large has been explained by the small and vice versa. Newton realized that the nature of gravity on Earth that pulls an apple to the ground could explain the motion of the moon and planets so much farther away. Minute atoms and molecules explain the chemistry of substances on a much larger scale. Decays of tiny nuclei explain the hot interior of the Earth. Fusion of nuclei likewise explains the energy of stars. Today, the patterns in particle physics seem to be explaining the evolution and character of the universe. And the nature of the universe has implications for unexplored regions of particle physics.

Cosmology is the study of the character and evolution of the universe. What are the major characteristics of the universe as we know them today? First, there are approximately [latex]{10^{11}}[/latex] galaxies in the observable part of the universe. An average galaxy contains more than [latex]{10^{11}}[/latex] stars, with our Milky Way galaxy being larger than average, both in its number of stars and its dimensions. Ours is a spiral-shaped galaxy with a diameter of about 100,000 light years and a thickness of about 2000 light years in the arms with a central bulge about 10,000 light years across. The Sun lies about 30,000 light years from the center near the galactic plane. There are significant clouds of gas, and there is a halo of less-dense regions of stars surrounding the main body. (See Figure 2.) Evidence strongly suggests the existence of a large amount of additional matter in galaxies that does not produce light—the mysterious dark matter we shall later discuss.

Distances are great even within our galaxy and are measured in light years (the distance traveled by light in one year). The average distance between galaxies is on the order of a million light years, but it varies greatly with galaxies forming clusters such as shown in Figure 1. The Magellanic Clouds, for example, are small galaxies close to our own, some 160,000 light years from Earth. The Andromeda galaxy is a large spiral galaxy like ours and lies 2 million light years away. It is just visible to the naked eye as an extended glow in the Andromeda constellation. Andromeda is the closest large galaxy in our local group, and we can see some individual stars in it with our larger telescopes. The most distant known galaxy is 14 billion light years from Earth—a truly incredible distance. (See Figure 3.)

Consider the fact that the light we receive from these vast distances has been on its way to us for a long time. In fact, the time in years is the same as the distance in light years. For example, the Andromeda galaxy is 2 million light years away, so that the light now reaching us left it 2 million years ago. If we could be there now, Andromeda would be different. Similarly, light from the most distant galaxy left it 14 billion years ago. We have an incredible view of the past when looking great distances. We can try to see if the universe was different then—if distant galaxies are more tightly packed or have younger-looking stars, for example, than closer galaxies, in which case there has been an evolution in time. But the problem is that the uncertainties in our data are great. Cosmology is almost typified by these large uncertainties, so that we must be especially cautious in drawing conclusions. One consequence is that there are more questions than answers, and so there are many competing theories. Another consequence is that any hard data produce a major result. Discoveries of some importance are being made on a regular basis, the hallmark of a field in its golden age.

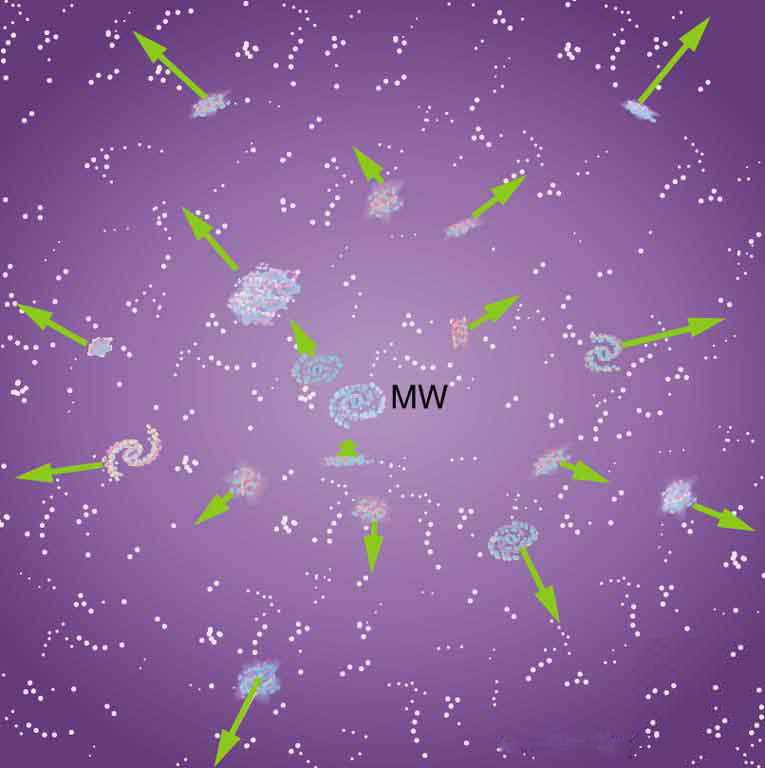
Perhaps the most important characteristic of the universe is that all galaxies except those in our local cluster seem to be moving away from us at speeds proportional to their distance from our galaxy. It looks as if a gigantic explosion, universally called the Big Bang, threw matter out some billions of years ago. This amazing conclusion is based on the pioneering work of Edwin Hubble (1889–1953), the American astronomer. In the 1920s, Hubble first demonstrated conclusively that other galaxies, many previously called nebulae or clouds of stars, were outside our own. He then found that all but the closest galaxies have a red shift in their hydrogen spectra that is proportional to their distance. The explanation is that there is a cosmological red shift due to the expansion of space itself. The photon wavelength is stretched in transit from the source to the observer. Double the distance, and the red shift is doubled. While this cosmological red shift is often called a Doppler shift, it is not—space itself is expanding. There is no center of expansion in the universe. All observers see themselves as stationary; the other objects in space appear to be moving away from them. Hubble was directly responsible for discovering that the universe was much larger than had previously been imagined and that it had this amazing characteristic of rapid expansion.

Universal expansion on the scale of galactic clusters (that is, galaxies at smaller distances are not uniformly receding from one another) is an integral part of modern cosmology. For galaxies farther away than about 50 Mly (50 million light years), the expansion is uniform with variations due to local motions of galaxies within clusters. A representative recession velocity [latex]{v}[/latex] can be obtained from the simple formula

[latex]{v=H_0d},[/latex]

where [latex]{d}[/latex] is the distance to the galaxy and [latex]{H_0}[/latex] is the Hubble constant. The Hubble constant is a central concept in cosmology. Its value is determined by taking the slope of a graph of velocity versus distance, obtained from red shift measurements, such as shown in Figure 4. We shall use an approximate value of [latex]{H_0=20\text{ km/s}\cdotp\text{Mly}}[/latex] . Thus, [latex]{v=H_0d}[/latex] is an average behavior for all but the closest galaxies. For example, a galaxy 100 Mly away (as determined by its size and brightness) typically moves away from us at a speed of [latex]{v=(20\text{ km/s}\cdotp\text{Mly})(100\text{ Mly})=2000\text{ km/s}}[/latex] . There can be variations in this speed due to so-called local motions or interactions with neighboring galaxies. Conversely, if a galaxy is found to be moving away from us at speed of 100,000 km/s based on its red shift, it is at a distance

[latex]{d=v/H_0=(10,000\text{ km/s})/(20\text{ km/s}\cdotp\text{Mly})=5000\text{ Mly}=5\text{ Gly}}[/latex] or [latex]{5\times10^9\text{ ly}}.[/latex] This last calculation is approximate, because it assumes the expansion rate was the same 5 billion years ago as now. A similar calculation in Hubble’s measurement changed the notion that the universe is in a steady state.

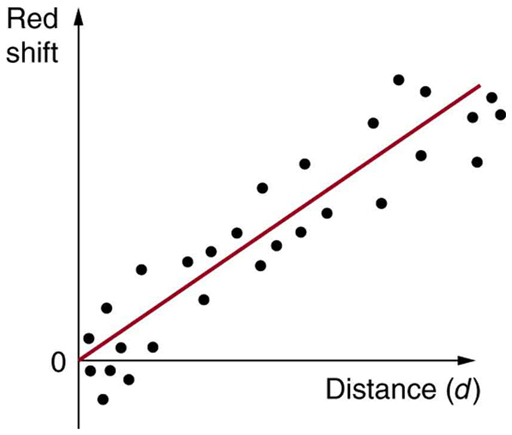
One of the most intriguing developments recently has been the discovery that the expansion of the universe may be faster now than in the past, rather than slowing due to gravity as expected. Various groups have been looking, in particular, at supernovas in moderately distant galaxies (less than 1 Gly) to get improved distance measurements. Those distances are larger than expected for the observed galactic red shifts, implying the expansion was slower when that light was emitted. This has cosmological consequences that are discussed in Chapter 34.4 Dark Matter and Closure. The first results, published in 1999, are only the beginning of emerging data, with astronomy now entering a data-rich era.

Figure 5 shows how the recession of galaxies looks like the remnants of a gigantic explosion, the famous Big Bang. Extrapolating backward in time, the Big Bang would have occurred between 13 and 15 billion years ago when all matter would have been at a point. Questions instantly arise. What caused the explosion? What happened before the Big Bang? Was there a before, or did time start then? Will the universe expand forever, or will gravity reverse it into a Big Crunch? And is there other evidence of the Big Bang besides the well-documented red shifts?

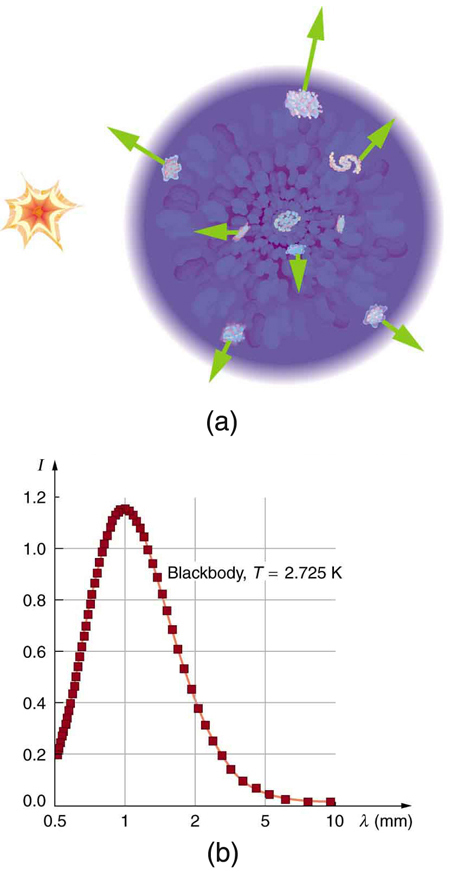
The Russian-born American physicist George Gamow (1904–1968) was among the first to note that, if there was a Big Bang, the remnants of the primordial fireball should still be evident and should be blackbody radiation. Since the radiation from this fireball has been traveling to us since shortly after the Big Bang, its wavelengths should be greatly stretched. It will look as if the fireball has cooled in the billions of years since the Big Bang. Gamow and collaborators predicted in the late 1940s that there should be blackbody radiation from the explosion filling space with a characteristic temperature of about 7 K. Such blackbody radiation would have its peak intensity in the microwave part of the spectrum. (See Figure 6.) In 1964, Arno Penzias and Robert Wilson, two American scientists working with Bell Telephone Laboratories on a low-noise radio antenna, detected the radiation and eventually recognized it for what it is.

Figure 6(b) shows the spectrum of this microwave radiation that permeates space and is of cosmic origin. It is the most perfect blackbody spectrum known, and the temperature of the fireball remnant is determined from it to be [latex]{2.725\:\pm\:0.002\text{ K}}[/latex] . The detection of what is now called the cosmic microwave background (CMBR) was so important (generally considered as important as Hubble’s detection that the galactic red shift is proportional to distance) that virtually every scientist has accepted the expansion of the universe as fact. Penzias and Wilson shared the 1978 Nobel Prize in Physics for their discovery.

Matter versus antimatter

We know from direct observation that antimatter is rare. The Earth and the solar system are nearly pure matter. Space probes and cosmic rays give direct evidence—the landing of the Viking probes on Mars would have been spectacular explosions of mutual annihilation energy if Mars were antimatter. We also know that most of the universe is dominated by matter. This is proven by the lack of annihilation radiation coming to us from space, particularly the relative absence of 0.511-MeV [latex]\gamma[/latex] rays created by the mutual annihilation of electrons and positrons. It seemed possible that there could be entire solar systems or galaxies made of antimatter in perfect symmetry with our matter-dominated systems. But the interactions between stars and galaxies would sometimes bring matter and antimatter together in large amounts. The annihilation radiation they would produce is simply not observed. Antimatter in nature is created in particle collisions and in [latex]\beta^{+}[/latex] decays, but only in small amounts that quickly annihilate, leaving almost pure matter surviving.

Particle physics seems symmetric in matter and antimatter. Why isn’t the cosmos? The answer is that particle physics is not quite perfectly symmetric in this regard. The decay of one of the neutral [latex]{K}[/latex] -mesons, for example, preferentially creates more matter than antimatter. This is caused by a fundamental small asymmetry in the basic forces. This small asymmetry produced slightly more matter than antimatter in the early universe. If there was only one part in [latex]{10^9}[/latex] more matter (a small asymmetry), the rest would annihilate pair for pair, leaving nearly pure matter to form the stars and galaxies we see today. So the vast number of stars we observe may be only a tiny remnant of the original matter created in the Big Bang. Here at last we see a very real and important asymmetry in nature. Rather than be disturbed by an asymmetry, most physicists are impressed by how small it is. Furthermore, if the universe were completely symmetric, the mutual annihilation would be more complete, leaving far less matter to form us and the universe we know.

How can something so old have so few wrinkles?

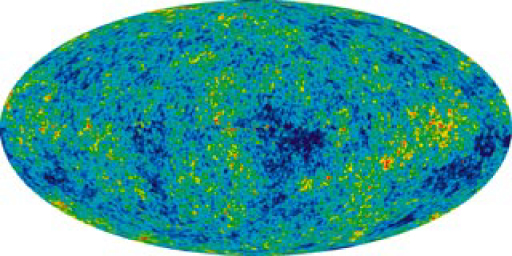
A troubling aspect of cosmic microwave background radiation (CMBR) was soon recognized. True, the CMBR verified the Big Bang, had the correct temperature, and had a blackbody spectrum as expected. But the CMBR was too smooth—it looked identical in every direction. Galaxies and other similar entities could not be formed without the existence of fluctuations in the primordial stages of the universe and so there should be hot and cool spots in the CMBR, nicknamed wrinkles, corresponding to dense and sparse regions of gas caused by turbulence or early fluctuations. Over time, dense regions would contract under gravity and form stars and galaxies. Why aren’t the fluctuations there? (This is a good example of an answer producing more questions.) Furthermore, galaxies are observed very far from us, so that they formed very long ago. The problem was to explain how galaxies could form so early and so quickly after the Big Bang if its remnant fingerprint is perfectly smooth. The answer is that if you look very closely, the CMBR is not perfectly smooth, only extremely smooth.

A satellite called the Cosmic Background Explorer (COBE) carried an instrument that made very sensitive and accurate measurements of the CMBR. In April of 1992, there was extraordinary publicity of COBE’s first results—there were small fluctuations in the CMBR. Further measurements were carried out by experiments including NASA’s Wilkinson Microwave Anisotropy Probe (WMAP), which launched in 2001. Data from WMAP provided a much more detailed picture of the CMBR fluctuations. (See Figure 6.) These amount to temperature fluctuations of only [latex]{200\:\mu{k}}[/latex] out of 2.7 K, better than one part in 1000. The WMAP experiment will be followed up by the European Space Agency’s Planck Surveyor, which launched in 2009.

Let us now examine the various stages of the overall evolution of the universe from the Big Bang to the present, illustrated in Figure 8. Note that scientific notation is used to encompass the many orders of magnitude in time, energy, temperature, and size of the universe. Going back in time, the two lines approach but do not cross (there is no zero on an exponential scale). Rather, they extend indefinitely in ever-smaller time intervals to some infinitesimal point.

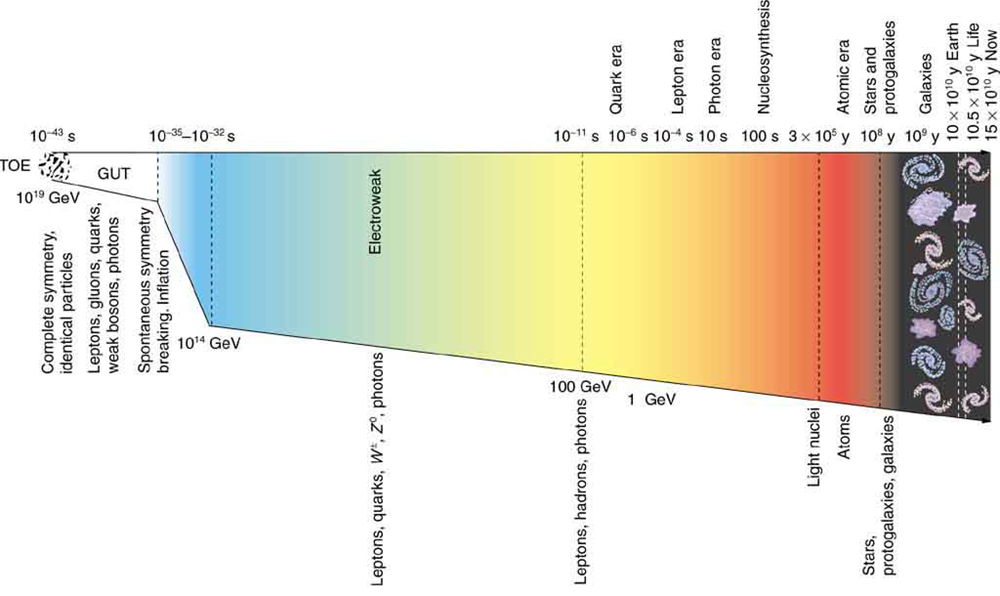
Going back in time is equivalent to what would happen if expansion stopped and gravity pulled all the galaxies together, compressing and heating all matter. At a time long ago, the temperature and density were too high for stars and galaxies to exist. Before then, there was a time when the temperature was too great for atoms to exist. And farther back yet, there was a time when the temperature and density were so great that nuclei could not exist. Even farther back in time, the temperature was so high that average kinetic energy was great enough to create short-lived particles, and the density was high enough to make this likely. When we extrapolate back to the point of [latex]{W^{\pm}}[/latex] and [latex]{Z^0}[/latex] production (thermal energies reaching 1 TeV, or a temperature of about [latex]{10^{15}\text{ K}}[/latex] ), we reach the limits of what we know directly about particle physics. This is at a time about [latex]{10^{-12}\text{ s}}[/latex] after the Big Bang. While [latex]{10^{-12}\text{ s}}[/latex] may seem to be negligibly close to the instant of creation, it is not. There are important stages before this time that are tied to the unification of forces. At those stages, the universe was at extremely high energies and average particle separations were smaller than we can achieve with accelerators. What happened in the early stages before [latex]{10^{-12}\text{ s}}[/latex] is crucial to all later stages and is possibly discerned by observing present conditions in the universe. One of these is the smoothness of the CMBR.

Names are given to early stages representing key conditions. The stage before [latex]{10^{-11}\text{ s}}[/latex] back to [latex]{10^{-34}\text{ s}}[/latex] is called the electroweak epoch, because the electromagnetic and weak forces become identical for energies above about 100 GeV. As discussed earlier, theorists expect that the strong force becomes identical to and thus unified with the electroweak force at energies of about [latex]{10^{14}\text{ GeV}}.[/latex] The average particle energy would be this great at [latex]{10^{-34}\text{ s}}[/latex] after the Big Bang, if there are no surprises in the unknown physics at energies above about 1 TeV. At the immense energy of [latex]{10^{14}\text{ GeV}}[/latex] (corresponding to a temperature of about [latex]{10^{26}\text{ K}}[/latex] ), the [latex]{W^{pm}}[/latex] and [latex]{Z^0}[/latex] carrier particles would be transformed into massless gauge bosons to accomplish the unification. Before [latex]{10^{-34}\text{ s}}[/latex] back to about [latex]{10^{-43}\text{ s}}[/latex] , we have Grand Unification in the GUT epoch, in which all forces except gravity are identical. At [latex]{10^{-43}\text{ s}}[/latex] , the average energy reaches the immense [latex]{10^{19}\text{ GeV}}[/latex] needed to unify gravity with the other forces in TOE, the Theory of Everything. Before that time is the TOE epoch, but we have almost no idea as to the nature of the universe then, since we have no workable theory of quantum gravity. We call the hypothetical unified force superforce.

Now let us imagine starting at TOE and moving forward in time to see what type of universe is created from various events along the way. As temperatures and average energies decrease with expansion, the universe reaches the stage where average particle separations are large enough to see differences between the strong and electroweak forces (at about [latex]{10^{-35}\text{ s}}[/latex] ). After this time, the forces become distinct in almost all interactions—they are no longer unified or symmetric. This transition from GUT to electroweak is an example of spontaneous symmetry breaking, in which conditions spontaneously evolved to a point where the forces were no longer unified, breaking that symmetry. This is analogous to a phase transition in the universe, and a clever proposal by American physicist Alan Guth in the early 1980s ties it to the smoothness of the CMBR. Guth proposed that spontaneous symmetry breaking (like a phase transition during cooling of normal matter) released an immense amount of energy that caused the universe to expand extremely rapidly for the brief time from [latex]{10^{-35}\text{ s}}[/latex] to about [latex]{10^{-32}\text{ s}}[/latex] . This expansion may have been by an incredible factor of [latex]{10^{50}}[/latex] or more in the size of the universe and is thus called the inflationary scenario. One result of this inflation is that it would stretch the wrinkles in the universe nearly flat, leaving an extremely smooth CMBR. While speculative, there is as yet no other plausible explanation for the smoothness of the CMBR. Unless the CMBR is not really cosmic but local in origin, the distances between regions of similar temperatures are too great for any coordination to have caused them, since any coordination mechanism must travel at the speed of light. Again, particle physics and cosmology are intimately entwined. There is little hope that we may be able to test the inflationary scenario directly, since it occurs at energies near [latex]{10^{14}\text{ GeV}}[/latex] , vastly greater than the limits of modern accelerators. But the idea is so attractive that it is incorporated into most cosmological theories.

Characteristics of the present universe may help us determine the validity of this intriguing idea. Additionally, the recent indications that the universe’s expansion rate may be increasing (see Chapter 34.4 Dark Matter and Closure) could even imply that we are in another inflationary epoch.

It is important to note that, if conditions such as those found in the early universe could be created in the laboratory, we would see the unification of forces directly today. The forces have not changed in time, but the average energy and separation of particles in the universe have. As discussed in Chapter 33.2 The Four Basic Forces, the four basic forces in nature are distinct under most circumstances found today. The early universe and its remnants provide evidence from times when they were unified under most circumstances.

Problems & Exercises

1: Find the approximate mass of the luminous matter in the Milky Way galaxy, given it has approximately [latex]{10^{11}}[/latex] stars of average mass 1.5 times that of our Sun.

2: Find the approximate mass of the dark and luminous matter in the Milky Way galaxy. Assume the luminous matter is due to approximately [latex]{10^{11}}[/latex] stars of average mass 1.5 times that of our Sun, and take the dark matter to be 10 times as massive as the luminous matter.

3: (a) Estimate the mass of the luminous matter in the known universe, given there are [latex]{10^{11}}[/latex] galaxies, each containing [latex]{10^{11}}[/latex] stars of average mass 1.5 times that of our Sun. (b) How many protons (the most abundant nuclide) are there in this mass? (c) Estimate the total number of particles in the observable universe by multiplying the answer to (b) by two, since there is an electron for each proton, and then by [latex]{10^9}[/latex] , since there are far more particles (such as photons and neutrinos) in space than in luminous matter.

4: If a galaxy is 500 Mly away from us, how fast do we expect it to be moving and in what direction?

5: On average, how far away are galaxies that are moving away from us at 2.0% of the speed of light?

6: Our solar system orbits the center of the Milky Way galaxy. Assuming a circular orbit 30,000 ly in radius and an orbital speed of 250 km/s, how many years does it take for one revolution? Note that this is approximate, assuming constant speed and circular orbit, but it is representative of the time for our system and local stars to make one revolution around the galaxy.

7: (a) What is the approximate speed relative to us of a galaxy near the edge of the known universe, some 10 Gly away? (b) What fraction of the speed of light is this? Note that we have observed galaxies moving away from us at greater than [latex]{0.9\text{ c}}[/latex] .

8: (a) Calculate the approximate age of the universe from the average value of the Hubble constant, [latex]{H_0=20\text{ km/s}\cdotp\text{Mly}}[/latex] . To do this, calculate the time it would take to travel 1 Mly at a constant expansion rate of 20 km/s. (b) If deceleration is taken into account, would the actual age of the universe be greater or less than that found here? Explain.

9: Assuming a circular orbit for the Sun about the center of the Milky Way galaxy, calculate its orbital speed using the following information: The mass of the galaxy is equivalent to a single mass [latex]{1.5\times10^{11}}[/latex] times that of the Sun (or [latex]{3\times10^{41}\text{ kg}}[/latex] ), located 30,000 ly away.

10: (a) What is the approximate force of gravity on a 70-kg person due to the Andromeda galaxy, assuming its total mass is [latex]{10^{13}}[/latex] that of our Sun and acts like a single mass 2 Mly away? (b) What is the ratio of this force to the person’s weight? Note that Andromeda is the closest large galaxy.

11: Andromeda galaxy is the closest large galaxy and is visible to the naked eye. Estimate its brightness relative to the Sun, assuming it has luminosity [latex]{10^{12}}[/latex] times that of the Sun and lies 2 Mly away.

12: (a) A particle and its antiparticle are at rest relative to an observer and annihilate (completely destroying both masses), creating two [latex]\gamma[/latex] rays of equal energy. What is the characteristic [latex]\gamma[/latex] -ray energy you would look for if searching for evidence of proton-antiproton annihilation? (The fact that such radiation is rarely observed is evidence that there is very little antimatter in the universe.) (b) How does this compare with the 0.511-MeV energy associated with electron-positron annihilation?

13: The average particle energy needed to observe unification of forces is estimated to be [latex]{10^{19}\text{ GeV}}[/latex] . (a) What is the rest mass in kilograms of a particle that has a rest mass of [latex]{10^{19}\text{ GeV/}c^2}[/latex] ? (b) How many times the mass of a hydrogen atom is this?

14: The peak intensity of the CMBR occurs at a wavelength of 1.1 mm. (a) What is the energy in eV of a 1.1-mm photon? (b) There are approximately [latex]{10^9}[/latex] photons for each massive particle in deep space. Calculate the energy of [latex]{10^9}[/latex] such photons. (c) If the average massive particle in space has a mass half that of a proton, what energy would be created by converting its mass to energy? (d) Does this imply that space is “matter dominated”? Explain briefly.

15: (a) What Hubble constant corresponds to an approximate age of the universe of [latex]{10^{10}}[/latex] y? To get an approximate value, assume the expansion rate is constant and calculate the speed at which two galaxies must move apart to be separated by 1 Mly (present average galactic separation) in a time of [latex]{10^{10}}[/latex] y. (b) Similarly, what Hubble constant corresponds to a universe approximately [latex]{2\times10^{10}}[/latex] -y old?

16: Show that the velocity of a star orbiting its galaxy in a circular orbit is inversely proportional to the square root of its orbital radius, assuming the mass of the stars inside its orbit acts like a single mass at the center of the galaxy. You may use an equation from a previous chapter to support your conclusion, but you must justify its use and define all terms used.

17: The core of a star collapses during a supernova, forming a neutron star. Angular momentum of the core is conserved, and so the neutron star spins rapidly. If the initial core radius is [latex]{5.0\times10^5\text{ km}}[/latex] and it collapses to 10.0 km, find the neutron star’s angular velocity in revolutions per second, given the core’s angular velocity was originally 1 revolution per 30.0 days.

18: Using data from the previous problem, find the increase in rotational kinetic energy, given the core’s mass is 1.3 times that of our Sun. Where does this increase in kinetic energy come from?

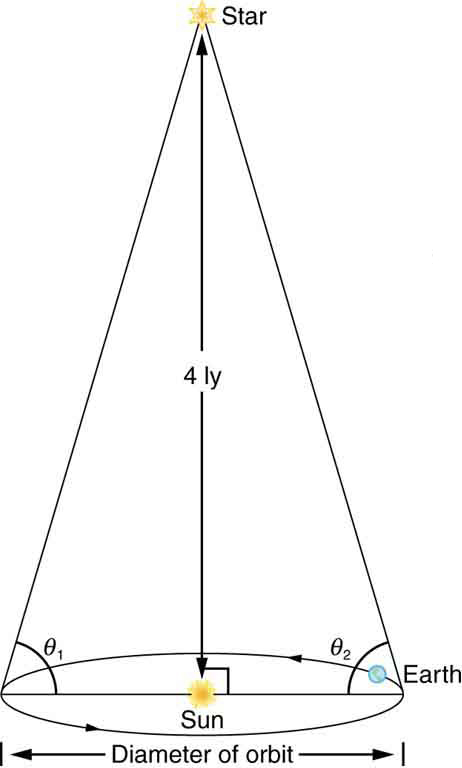
19: Distances to the nearest stars (up to 500 ly away) can be measured by a technique called parallax, as shown in Figure 9. What are the angles [latex]{\theta _1}[/latex] and [latex]{\theta_2}[/latex] relative to the plane of the Earth’s orbit for a star 4.0 ly directly above the Sun?

20: (a) Use the Heisenberg uncertainty principle to calculate the uncertainty in energy for a corresponding time interval of [latex]{10^{-43}\text{ s}}[/latex] . (b) Compare this energy with the [latex]{10^{19}\text{ GeV}}[/latex] unification-of-forces energy and discuss why they are similar.

21: Construct Your Own Problem

Consider a star moving in a circular orbit at the edge of a galaxy. Construct a problem in which you calculate the mass of that galaxy in kg and in multiples of the solar mass based on the velocity of the star and its distance from the center of the galaxy.