Imprinted atomic displacements drive spin–orbital order in a vanadate perovskite

Perovskites have important applications in diverse areas, including catalysis¹, photovoltaics² and electronics³. The versatility of this structural type derives from the possibility of tuning both the density of mobile charge carriers and the strength and anisotropy of electron-transfer parameters between atomic sites. Explorations of the physical properties of perovskite compounds have usually proceeded by chemical substitution of bulk samples. A well-known example of correlated electron materials is the RVO₃ family of Mott insulators (where R is a trivalent rare earth). Upon changing the size of the R cations and the consequent modulation of the vanadium oxide bond network, different magnetic and orbital ordering patterns are observed⁴ that lead to unusual macroscopic magnetic properties⁵. In bulk synthesis, however, only a limited number of phases can be stabilized with the available growth parameters such as temperature or pressure, and chemical substitution in doped variants often leads to structural and electronic disorder.

Advances in the synthesis of epitaxial thin films and heterostructures have recently enabled a new set of control capabilities. For instance, interfacial charge transfer can tune the charge carrier density without introducing structural disorder³ and substrate-induced biaxial strain could stabilize new phases through modification of bond lengths and angles^6,7,8. A less explored effect in epitaxy is the influence of non-cubic crystal facets and the associated determination of the directions along which the biaxial constraints act and which direction is free to adapt. Previous research has focused on comparing films grown on different pseudocubic (pc) facets, such as (001)_pc, (110)_pc and (111)_pc (Fig. 1a), that provide different surface symmetries^9,10,11,12. However, the net charges of the atomic layers parallel to the substrate depend entirely on the particular pseudocubic facet ((001)_pc, (110)_pc or (111)_pc), which can lead to distinct polarity discontinuities at the interface and, thus, to different electronic interfacial reconstructions⁹. Furthermore, the lattice mismatch is often very different for different facets. As with bulk synthesis, disentangling the structural from the electronic effects has proven to be difficult.

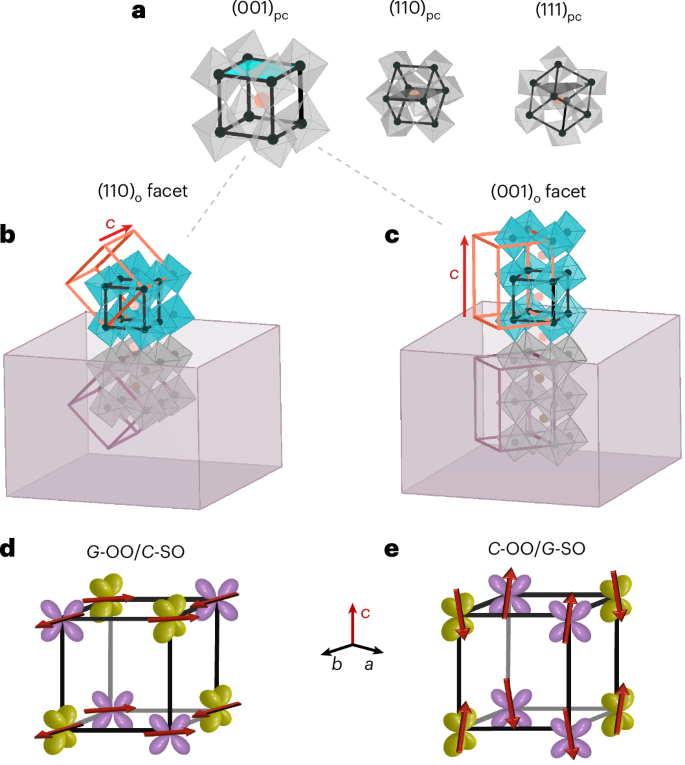
a, Commonly used pseudocubic (001)_pc, (110)_pc and (111)_pc facets. The (001)_pc facet used in this study, which corresponds to the two orthorhombic facets in b and c, is highlighted in blue. b,c, The epitaxial growth of YVO thin films on YAO substrates with orthorhombic orientations (110)_o (b) and (001)_o (c) enables the stabilization of the G-OO/C-SO and C-OO/G-SO phases, respectively. The two facets are indistinguishable in the cubic approximation and correspond to the (001)_pc facet, as indicated by the grey dashed lines. The blue and grey octahedra represent the film and substrate, respectively. The orthorhombic and pseudocubic unit cells of the film are shown in orange and black, respectively. The film orthorhombic unit cell aligns with that of the substrate, shown in maroon. d,e, G-OO/C-SO (d) and C-OO/G-SO (e) spin–orbital phases of bulk RVO₃. The xz and yz orbitals are shown in yellow and purple and red arrows indicate the spin at each site.

Here we separate these effects and illustrate how even the very subtle changes associated with facets that are indistinguishable in the cubic frame can have a notable ability to alter the phase diagram of transition-metal oxides and stabilize competing phases. Thus, we synthesized films on two facets of orthorhombic YAlO₃ (YAO), both of which correspond to a (001)_pc surface, have identical polarities and almost the same in-plane lattice mismatch with YVO₃ (YVO). These facets, therefore, differ almost exclusively in the subtle octahedral rotation and cation displacement patterns exposed at the substrate surface and imprinted in the films. The detection of staggered magnetic and orbital order in these films presents another set of challenges, as the X-ray diffraction (XRD) and neutron scattering methods used for this purpose in bulk¹³ are not applicable due to the small sample volume available. Therefore, we used confocal Raman spectroscopy, which was developed to study thin films¹⁴, to investigate specific vibrational modes that are characteristic for different types of orbital order¹⁵ and employed spectroscopic ellipsometry to identify optical signatures of different antiferromagnetic orders. Notably, we found that different spin–orbital order patterns were realized in YVO grown on the two different YAO(001)_pc facets. The orthorhombic structure of YVO and the consequent anisotropy of electronic properties are very common in several families of ABO₃ compounds. Therefore, using different orthorhombic facets that are indistinguishable in the cubic setting to manipulate and study the phase diagram in a controlled manner is widely applicable to other orthorhombic correlated oxides with anisotropic properties.

In bulk form, the C-type orbital order (OO) and G-type spin order (SO), shown in Fig. 1e, form the ground state of YVO₃. Heating above T_OO2/SO2 = 77 K induced a first-order phase transition into a state with G-type orbital and C-type spin order (Fig. 1d). Both forms of order disappeared upon further heating above the Néel temperature at T_SO1 = 116 K and the orbital ordering temperature at T_OO1 = 200 K, respectively^15,16,17. This sequence of transitions has been ascribed to the interplay of crystal-field effects and superexchange interactions, but many aspects of the underlying energetics remain unresolved.

Bulk YVO has an orthorhombic Pbnm space group at room temperature, with lattice parameters a = 5.279 Å, b = 5.611 Å and c = 7.572 Å (ref. ¹⁸). We synthesized a series of YVO thin films on substrate materials have the same Pbnm structure, in particular YAlO₃ (YAO). The two facets, YAO(110)_o and YAO(001)_o, exert compressive strains on YVO that are almost identical, as indicated by the lattice mismatch¹⁹ shown in the schematics in Fig. 2a,b. Results for other films on NdGaO₃(110)_o (NGO) and DyScO₃(110)_o (DSO) that were subjected to different tensile strains are shown in Extended Data Figs. 1 and 2. XRD revealed that for all the samples, the orientation of the unit cell of the single-domain YVO film followed that of the substrate facet, so that the c axis was parallel to that of the substrate (Extended Data Fig. 1). Consequently, the film c axis was in the plane for (110)_o-oriented substrates and out of plane for (001)_o-oriented substrates. Further, the film on NGO(110)_o was fully epitaxially grown, whereas the films on YAO(110)_o, YAO(001)_o and DSO(110)_o were partially relaxed, due to the larger lattice mismatch (Supplementary Information, section I).

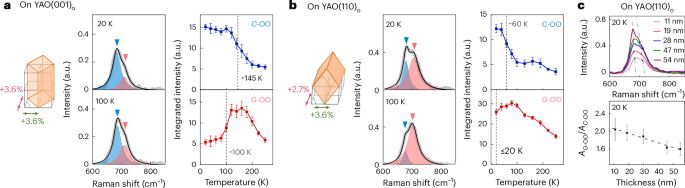
a,b, Schematics displaying the lattice mismatch of YVO (given by (a_l − a_s)/a_s, where a_l and a_s are the in-plane lattice parameters of bulk YVO and the substrate, respectively¹⁹) (left), Raman spectra of the B_1g mode at low and high temperatures (centre), integrated intensities of the C-OO phonon (top right) and the G-OO phonon (bottom right) of a YVO film on YAO(001)_o (a) and YAO(110)_o (b) substrates. The error bars denote the standard error for the derived ‘peak area’ parameters of the Voigt profiles fitted to the C-OO peaks (blue triangles) and G-OO peaks (pink triangles) (Methods). The dashed lines indicate the T_OO2/SO2 temperature of the transition from the C-OO/G-SO ground state to the G-OO/C-SO intermediate-temperature state. c, Top, spectra of the B_1g mode at 20 K for YVO films with different thicknesses on YAO(110)_o. Bottom, ratio of integrated intensities of the G-OO phonon to that of the C-OO phonon and a linear fit.

To probe the orbital order of the YVO films, we performed polarized, confocal Raman spectroscopy. Previous Raman scattering studies on bulk YVO single crystals have identified two B_1g V–O stretching phonons around 83 and 86 meV that couple with the C-type and G-type OO patterns, respectively¹⁵. The C-OO phonon was observed in the low-temperature C-OO/G-SO phase, and there was a sharp drop in its intensity above the first-order phase transition at 77 K (T_OO2/SO2) to the G-OO/C-SO phase. At this temperature, the G-OO mode appeared abruptly and gradually lost intensity with increasing temperature, disappearing above 200 K (T_OO1), where the second-order phase transition to the disordered phase occurred. Both modes were observed in the y(xx)y polarization configuration (x ∥ a + b, y ∥ a − b, where x and y are pseudocubic directions).

Figure 2a,b displays the Raman measurements of YVO thin films of ~30 nm thickness, grown on YAO(001)_o and YAO(110)_o substrates, respectively. For each sample, the B_1g spectra and temperature dependence of the phonon mode intensities are shown on the centre and right sides of the panel, respectively. The spectra at each temperature were fitted with two Voigt profiles (convolutions of Gaussian and Lorentzian functions) for the C-OO phonon (blue triangle) and G-OO phonon (pink triangle).

For the film on YAO(001)_o (Fig. 2a), we found two peaks in the expected energy range, which we identified as the lower-energy C-OO mode and the higher-energy G-OO mode. Their temperature dependences were qualitatively similar to that of bulk YVO. The C-OO mode was more intense at low temperatures and decreased at higher temperatures, whereas the G-OO mode showed the opposite behaviour. As the first-order transition at T_OO2/SO2 was accompanied by a strong change in the C-OO and G-OO mode intensities, we estimated the transition temperature by taking the derivative of the phonon integrated intensities (Supplementary Information, section II).

Note two distinct differences in the phonon spectra of the film compared to bulk YVO. First, the transition temperatures obtained from both the C-OO and G-OO modes were considerably higher than the bulk value of T_OO2/SO2. This indicates that the C-OO phase was enhanced in the film on YAO(001)_o. Second, note that, unlike in bulk YVO, there was a substantial mismatch between the transition temperatures obtained from the C-OO and G-OO modes. This was a consequence of the gradual relaxation of the imprinted atomic displacements, which created a temperature range in which both phases coexisted. Between 100 and 145 K, the C-OO phase was stabilized in the layers close to the substrate that exhibited coherently imprinted structural distortions, whereas the layers farther from the substrate showed progressively more bulk-like behaviour. The concurrent effects of the gradient of imprinted atomic displacements along with the phase stabilization created the observed difference in T_OO2/SO2 values obtained from the two modes, which further supports the inference of said phase stabilization.

For the film on YAO(110)_o (Fig. 2b), the temperature dependence of the C-OO phonon was qualitatively like that of the bulk but yielded T_OO2/SO2 ≈ 60 K, which is lower than that of the bulk. By contrast, the temperature dependence of the G-OO phonon appeared markedly different compared to bulk YVO¹⁵. At the lowest temperature measured (20 K), the intensity was large and stayed nearly constant up to about 100 K, yielding T_OO2/SO2 ≈ 20 K. This suggests that the G-OO phase was favoured in this case, in stark contrast to the film on YAO(001)_o, where the competing C-OO phase was stabilized. As with the film on YAO(001)_o, the observed difference in T_OO2/SO2 was attributed to the concurrent effects of the relaxation gradient and phase stabilization. A comparison of the thickness-dependent Raman spectra of YVO films on YAO(110)_o and NGO(110)_o revealed that the ratio of the C-OO peak intensity to the G-OO peak intensity increased with a reduction of the film thickness for the films on YAO(110)_o and remained unchanged for the film on NGO(110)_o (Fig. 2c and Supplementary Information, section III). This observation further validated that the phase stabilization was, indeed, a result of the imprinted atomic displacements from the substrate, as only the films on YAO(110)_o have a gradient of said displacements. The influence of the substrate facets, which differed only in subtle orthorhombic distortions, were, therefore, extremely consequential in determining the properties of the YVO films, as they exhibited essentially different ground states on the same substrate material.

Finally, to determine whether the structural phase transitions indicated by the OO-coupled phonons were also associated with electronic structure changes, as in bulk YVO, we used ellipsometry to measure the temperature-dependent optical conductivity spectra of a YVO film on YAO(110)_o (48 nm thickness). Figure 3b displays the temperature dependence of the real part of the optical conductivity \({\sigma}_{1}^{\,c}\) along the c axis. The positions of the multiplet peaks (A–D) match well with those of bulk YVO, for which mainly four peaks were identified¹⁷ (caption of Fig. 3). The trends for peaks A and B (high-spin multiplet) and peak C (low-spin multiplet) (Fig. 3a) have opposite temperature dependences (Supplementary Information, section IV), like bulk YVO, which confirms that the film, indeed, exhibited the electronic phase transitions corresponding to the phonon behaviour deduced from the Raman spectra. In particular, note that the optical spectra also shed light on the magnetic phase transition at T_OO2/SO2.

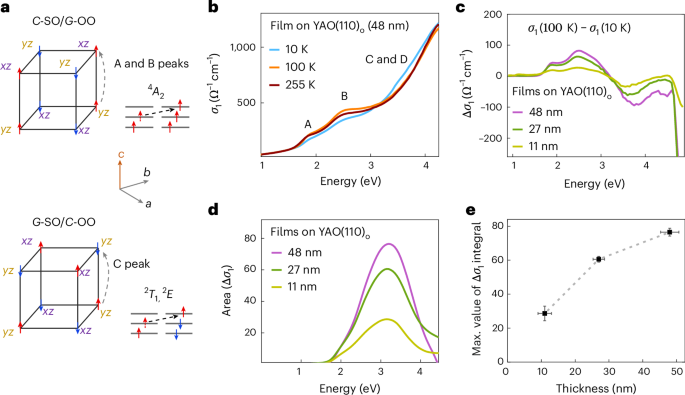
a, Spin–orbital configurations of C-SO/G-OO and G-SO/C-OO phases and multiplet configurations of optical transitions along the c axis, corresponding to peaks A, B and peak C. In bulk YVO, there are four multiplet peaks (A–D). Peaks A and B are associated with the high-spin ground state ⁴A₂ and peak C with the low-spin ²E and ²T₁ multiplets¹⁷. Peak D is assigned to t_2g to e_g transitions. b, Real part of the optical conductivity measured along the c axis for a 48-nm-thick YVO film on YAO(110)_o. c, Difference spectra of \({\sigma }_{1}^{\,{\mathrm{c}}}(100\,{\mathrm{K}})-{\sigma }_{1}^{\,{\mathrm{c}}}(10\,{\mathrm{K}})\) for YVO films on YAO(110)_o for different thicknesses. d, Integral of \({\sigma }_{1}^{\,{\mathrm{c}}}(100\,{\mathrm{K}})-{\sigma }_{1}^{\,{\mathrm{c}}}(10\,{\mathrm{K}})\) for YVO films on YAO(110)_o for different thicknesses. e, Maximum (max.) value of the Δσ₁ integral (curve d) versus the thickness of films on YAO(110)_o. The horizontal error bars indicate the standard deviation of the average thickness obtained from measurements of the distances of the Laue fringes around (00l)_pc Bragg reflections for each sample (Extended Data Fig. 1). The vertical error bars for the maximum value of the Δσ₁ integral were estimated by extracting σ₁ from a layer-on-substrate model in which the layer thickness was varied within the error bar.

To investigate the effect of epitaxy with the substrate, we compared the integral of \({\sigma }_{1}^{\,{\mathrm{c}}}\)(100 K) − \({\sigma }_{1}^{\,{\mathrm{c}}}\)(10 K) for films of various thicknesses grown on YAO(110)_o (Fig. 3d). The height of this curve represents the strength of the transition at T_OO2/SO2 (ref. ²⁰). The decreasing trend (Fig. 3e) as the film thickness was reduced suggests that as the film became thinner, this phase transition was increasingly suppressed. This observation is in complete accordance with the thickness-dependent phonon behaviour (Fig. 2c) and is a consequence of the G-OO/C-SO phase stabilization. Due to the gradient of imprinted atomic displacements, the fraction of the film that can contribute to the intensity reduces with the thickness of the film. Thus, the ellipsometry results complement the conclusions drawn from Raman spectroscopy and indicate a stabilization of the G-OO and corresponding C-SO phase for YVO on YAO(110)_o film. The extrapolation of the thickness dependence suggests that for films below 10 nm thickness the C-OO/G-SO phase would be on the verge of complete suppression as the spectral weight approaches zero. This suggests that multilayers may be able to entirely stabilize this phase, so that ultra-thin layers of the film could be epitaxially stabilized by sandwiching them between spacer layers²¹.

To understand the mechanism of epitaxial stabilization of the spin–orbital phases, we considered superexchange interactions and lattice effects. The Hamiltonian for the RVO₃ compounds, as proposed by Khaliullin²², is H = H_J + H_V, and consists of two terms representing each part, respectively. For the superexchange term H_J, considered in isolation, the lowest-energy phase corresponds to a G-OO/C-SO state^22,23. On the other hand, the lattice term H_V is a phenomenological term that supports the C-OO/G-SO phase and contains all the interactions arising from coupling to the lattice, including Jahn–Teller distortions, octahedral rotations and R–O covalency effects^22,24,25. Theoretical studies of RVO₃ using model Hamiltonians indicated that when H_J dominates, the G-OO/C-SO phase is favoured, whereas when H_V dominates, the C-OO/G-SO phase is favoured²².

Let us consider the effect of compression of a lattice parameter on the superexchange interactions acting along that direction. The superexchange coupling has the form J ∝ t²/U, where t is the effective d–d hopping amplitude (through O 2p) and U is the V 3d on-site Coulomb repulsion²⁶. Density functional theory studies of the related compounds LaVO₃ and YTiO₃ showed that a decrease in a lattice parameter along any direction produces shorter V–O bond lengths and smaller V–O–V bond angles along that direction²⁷. Shorter bond lengths increase the overlap of the V 3d and O 2p orbitals and produce larger effective d–d hopping amplitudes, whereas smaller bond angles result in less overlap and correspondingly reduce t. These effects have opposite trends and the same follows analogously for an expansion of a lattice parameter. Thus, bond lengths and bond angles contribute oppositely to t for a given change in a lattice parameter. However, density functional theory also emphasized that the effects of a change of the bond length on t dominate over the effects of changes to the bond angle in these compounds. Therefore, c-axis compression was expected to enhance J along this axis through a reduction in the bond length. Additionally, model Hamiltonian calculations of RVO₃ revealed that the orbital exchange constant along the c axis is about ten times larger than that in the a–b plane for the G-OO/C-SO phase^22,23. As orbital exchange is simply the orbital part of the superexchange interaction derived for a fixed spin order, the anisotropy of the orbital exchange constants is also transferred to the superexchange constants. Thus, any change in bond lengths along the c axis is more consequential for J than those in the a–b plane. The enhancement of J along the c axis, therefore, provides a reasonable explanation for the G-OO phase stabilization in (110)_o-oriented compressively strained films.

The lattice term H_V was determined from several effects that together favour the C-OO state, which, in turn, stabilized the G-SO state by coupling to it through Goodenough–Kanamori–Anderson rules. Hartree–Fock calculations performed for ABO₃ perovskites²⁸ and hydrostatic pressure studies performed on single crystals of YVO (refs. ^29,30) suggested that, of these effects, the A–O covalency made a dominant contribution. The calculations revealed that the d-type Jahn–Teller distortion corresponding to the C-OO phase becomes lower in energy than the a-type Jahn–Teller distortion (associated with the G-OO phase) only when the A–O covalency is included in the calculations. The energy of the d-type distortion was lowered, because it involves A-cation displacements that reduce the average A–O nearest neighbour distances and lower the energy of the C-OO phase, due to increased A–O hybridization. Furthermore, this displacement must necessarily take place roughly along the Pbnm b axis.

Figure 4 depicts the effect of A–O covalency in YVO films for the different facets considered here. The lattice mismatch in the (110)_o orientation is accommodated by increasing the atomic distances along a − b and decreasing them along a + b, as indicated by the green and pink arrows in Fig. 4a,b. Therefore, in general, we would expect this term to remain relatively unchanged for this orientation. For the (001)_o-oriented film, the distances along both directions a + b and a − b decrease, leading to a net reduction of bond distances along the relevant b direction, which enhances the lattice contribution that stabilizes the C-OO phase. Our analysis of the XRD data shows that the b lattice parameter is close to that of the bulk in the film on YAO(110)_o, whereas it is clearly compressed in the film on YAO(001)_o, as expected (Extended Data Fig. 1). Altogether, the enhancement of lattice effects and reduction of superexchange interactions due to increased atomic distances along the c axis provide a straightforward explanation for the C-OO phase stabilization on YAO(001)_o.

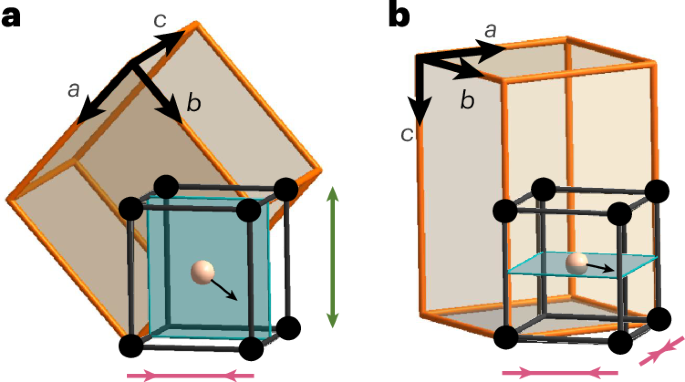
a,b, Difference in cation displacements in YVO (Y ions in orange, and V ions in black) on YAO (110)_o (a) and YAO (001)_o (b) substrate facets. The orthorhombic and pseudocubic unit cells are shown in orange and black, respectively. The small black arrows indicate the direction of the yttrium displacements. The Y–O distances are expected to remain relatively unchanged in a, as the increase in atomic distances along a + b (green arrow) is compensated for by the decrease along a − b (pink arrow). By contrast, in b, distances along both directions decrease.

In conclusion, our study of an epitaxial film of YVO demonstrates how specific octahedral rotation and cation displacement patterns in perovskites can be imprinted by the choice of the substrate facet and allows access to different phases. We attribute the observed stabilization of the different ground states exclusively to changes in superexchange interactions and lattice effects, which are imprinted by the different epitaxy on facets that are only distinguishable in their orthorhombic distortions.

As the relevant structural distortions and anisotropic properties investigated here are typical for transition-metal perovskites, the presented mechanism for material design is applicable for various epitaxial heterostructures, including titanates, chromates and manganites. In addition, a similar experimental methodology for detecting the effects of anisotropically imprinted atomic displacements will provide important insights into how heterostructuring alters the electronic phases in these systems. As such, this study broadens the perspective for a targeted manipulation of functional properties in quantum materials, such as colossal magnetoresistance in manganites³¹, piezoelectricity in perovskite nitrites³², tunable bandgaps of transparent conducting oxides^33,34 and perovskite-based photovoltaics^2,35,36.