Superconducting qubits can be fabricated and controlled in large numbers, which makes them an appealing platform for quantum simulations of many-body physics. However, a scalable way of implementing electromagnetism has been lacking — until now.
It has long been anticipated that quantum mechanical systems will provide an efficient way to solve intrinsically quantum mechanical problems1. Massive efforts have gone into developing quantum platforms that contain large numbers of well-controlled degrees of freedom, suitable for running algorithms or exploring many-body physics. Often quantum simulators are realized with electrically neutral degrees of freedom, which helps isolate them from environmental noise. However, this means that simulating the physics of electromagnetism requires the development of synthetic gauge fields within the quantum simulator. Writing in Nature Physics, Ilan Rosen and co-workers have now produced synthetic electromagnetic gauge fields for superconducting qubits in a scalable two-dimensional array2.
The short timescales of electron dynamics and the difficulty in controlling and understanding all aspects of a material system can make it challenging to gain new insights into solid-state physics. The field of quantum simulation has long had the goal of reproducing the physics of solid-state devices using alternative degrees of freedom, such as ultracold atoms or qubits in a quantum computer. Rosen and colleagues use the bosonic collective excitations of a superconducting qubit design known as a transmon.
If successful, the synthetic ‘electrons’ will experience the same kinds of Hamiltonians found in real materials, but in a context where dynamics are slow enough to be easily measured and in which the microscopic parameters of the Hamiltonian are all known. Measurements that are infeasible in a real material, such as mapping out the momentum distribution of a multi-‘electron’ state, are possible with a quantum simulation3; and experiments that would have required femto- or picosecond pulsed lasers in the solid state can be carried out with conventional digital and analogue electronics3.
However, achieving these abilities requires developing large-scale, well-controlled quantum systems and then introducing ingredients from solid-state physics, such as lattice potentials and electromagnetism. Many of the most well-established quantum simulation platforms involve degrees of freedom that are charge neutral. As a result, simulating electromagnetism requires gauge fields that produce dynamics identical to those expected from Maxwell’s equations, but for a completely different set of physical quantities.
In many cases, the degrees of freedom used for quantum simulation have inter-particle interactions that can simulate the repulsive Coulomb interactions. However, including the influence of external magnetic fields is essential for a full description of electronic behaviour, and there are not any easy analogues for neutral particles.
Methods for simulating electromagnetism by creating synthetic, effective, magnetic vector potentials have been developed for some quantum platforms, such as ultracold atoms4 and photonics5. Rosen and colleagues successfully produced a full set of synthetic external electric and magnetic fields for a four-by-four array of transmon superconducting qubits (see Fig. 1)2.
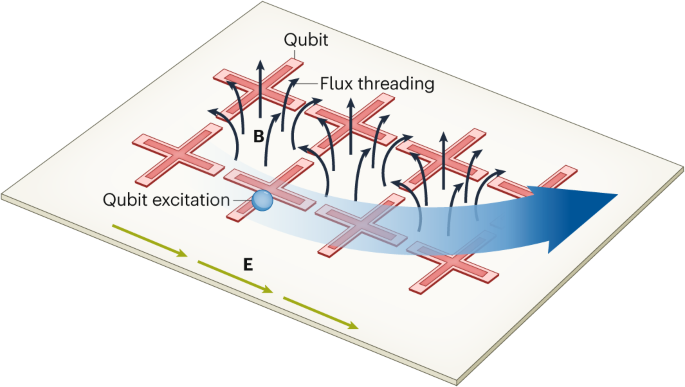
The excitations of transmon qubits arranged in a lattice (red crosses) can be used to perform quantum simulations of two-dimensional many-body physics models. However, the excitations are neutral and, to avoid the effects of noise, are specifically designed to be insensitive to electromagnetic fields in their environment This makes it difficult to simulate the important effects of external electric and magnetic fields on electrons. Rosen and colleagues’2 device allowed them to parametrically modulate the interactions between each pair of transmons, yielding a scalable method to produce effective electric (E, green arrows) and magnetic fields (B, black arrows) for transmon excitations. Among other phenomena, the team could observe the transmon excitations (blue circle) moving in curved trajectories (thick blue line) due to the classical Hall effect.
In classical mechanics, electromagnetism is usually formulated in terms of electromagnetic fields or scalar and vector potentials. However, the magnetic field can also be described using the Aharonov–Bohm effect, in which the wave function of a charged particle picks up a geometric phase when moving around an area penetrated by magnetic fields.
In lattice models, an equivalent phase can be produced by adding non-trivial so-called Peierls phases to the hopping terms in the Hamiltonian that cause excitations to move between lattice sites6,7. Rosen and colleagues2 directly implemented Peierls phases in the couplings between their qubits using a technique called parametric modulation, in which individual qubits are driven by microwave radiation, causing the energy levels of the qubit to oscillate at the microwave frequency. This frequency modulation of one qubit induces an effective coupling to its neighbours, with the amplitude and, crucially, the phase determined by the applied modulation.
Similar parametric modulation methods have been used to implement Peierls phases for superconducting qubits on a smaller scale, such as in a single ring8. However, they are typically costly in control complexity, for example by requiring a dedicated microwave control line for each pair of qubits to generate the coupling between them. This hardware-complexity cost has prevented scalable two-dimensional implementations until now. Rosen and colleagues overcame these challenges with a two-layer design that allows individual control and readout to be routed from above to all sixteen qubits arranged in a four-by-four array.
Because the Peierls phases that produce the effective magnetic field and vector potential are set by externally applied radio frequency driving fields, these phases can be varied in time, producing a time-varying vector potential — an effective electric field. Rosen and colleagues confirmed that the qubit excitations in the device display three canonical effects experienced by electrons in solids when subjected to electromagnetic fields. First, the Aharonov–Bohm effect, which they observed as magnetic-field-dependent interference in particle transport. Secondly, Wannier–Stark localization, in which the lattice structure prevents particles from moving under an applied electric field. Finally, the team observed the classical Hall effect, in which a longitudinal electric field and perpendicular magnetic field give rise to net transverse motion8.
Rosen and colleagues’ realization of a full set of effective electromagnetic fields is a major step forward in the field of superconducting circuits, where control complexity and the challenge of accessing centrally located qubits in the center of two-dimensional arrays are often the limiting factors.
The team’s four-by-four array is not large compared to the hundreds or thousands of sites available in neutral-atom lattice simulators, let alone compared to the enormous number of atoms and electrons in real materials. However, implementing effective gauge potentials at this scale, with qubits arranged in a two-dimensional lattice, means that many obstacles to larger-scale devices have been overcome. Furthermore, superconducting qubit devices have intrinsic time scales in the nanosecond to microsecond range, enabling much faster simulations than is possible in ultracold-atom synthetic gauge-field systems.
It should also be possible to realize strong inter-particle interactions in future generations of the experiment. Synthetic gauge fields have existed in photonics5 and ultracold atoms3,4 for some time, but both of these platforms intrinsically host only weak inter-particle interactions. By contrast, the transmon superconducting qubits used by Rosen and colleagues are highly nonlinear, with a strong, attractive effective interaction between the transmons’ excitations. The phenomenology and microscopic behaviour of the Hall effect has been studied extensively for the case of repulsively interacting fermions, but the Hall effect for bosonic particles with attractive interactions, such as those native to transmon qubits, is less well understood. As the push for quantum computing continues to increase the scale and performance of superconducting circuits, Rosen and colleagues’ work is a taste of what is to come for quantum simulation.